Grupa rapido

Frekvenca varianco en grupoj de gravitaj ondoj sur la surfaco de profunda akvo. La ruĝa punkto moviĝas kun la faza rapido, kaj la verdaj punktoj propagas kun la grupa rapido. En ĉi tiu profunda-akva okazo, la faza rapido estas dufoje pli granda ol la grupa rapido. La ruĝa punkto pasas du verdajn punktojn dum moviĝo de la maldekstro dekstren en la figuro.
Novaj ondoj aspektas al aperi dorse de onda grupo, kreski en amplitudo ĝis kiam ili estas je la centro de la grupo, kaj malaperi je la onda grupa antaŭo.
Por surfacaj gravitaj ondoj, la akvaj partiklaj rapidoj estas multe pli malgranda ol la faza rapido, en plej parto de la okazoj.

Ondo kun la grupa rapido kaj faza rapido irantaj en malsama direktoj. La grupa rapido estas pozitiva kaj la faza rapido estas negativa.

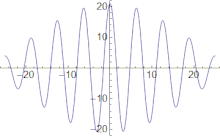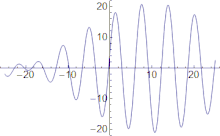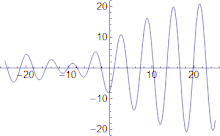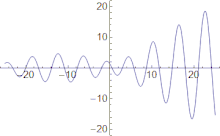
La grupa rapido de ondo estas la rapido kun kiu la entuta formo de la ondaj amplitudoj propagas tra spaco. La formo de la ondaj amplitudoj estas sciata kiel la modulado aŭ koverto de la ondo.

Ekzemple, imagu kio okazas se ŝtono estas ĵetita enen la mezon de lago. Kiam la ŝtono batas la surfacon de la akvo, cirkla ŝablono de ondoj aperas. Ĝi baldaŭ iĝas cirklan ringon de ondoj kun senmova centro. La elvolvanta ringo de ondoj estas la onda grupo, en kiu povas esti distingaj apartaj ondosimilaĵoj de malsamaj ondolongoj vojaĝantaj je malsamaj rapidoj. La pli longaj ondoj vojaĝi pli rapide ol la grupo entute, sed ili estingiĝas kiam ili proksimiĝas la antaŭ rando de la grupo (ekstera rando de la ringo). La pli mallongaj ondoj vojaĝi pli malrapide kaj ili estingiĝas kiam ili aperi de la malantaŭa rando de la grupo (ena rando de la ringo).

Difino

La grupa rapido v_g estas difinita per la ekvacio

$v_{g}={\frac {\partial \omega }{\partial k}}$

kie ω estas la onda angula frekvenco (kutime esprimita en radianoj por sekundo);

k estas la angula ondonombro (kutime esprimita en radianoj por metro).

La funkcio ω(k), kiu donas ω kiel funkcio de k, estas sciata kiel la varianca rilato. Se ω estas proporcia kun k, do la grupa rapido estas akurate egala al la faza rapido. Alie, la koverto de la ondoj estos malformigita kiam ĝi propagas. Ĉi tiu "grupa rapida varianco" estas grava efiki en la disvastigo de signaloj tra optika fibro kaj en la dizajno de alta-povumaj, mallonga-pulsaj laseroj.

La pli supre donita difino de grupa rapido estas nur utila por ondopakaĵoj, kiu estas pulsa tio estas kompakte lokigita en ambaŭ reala spaco kaj frekvenca spaco. Ĉar ondoj je malsamaj frekvencoj propagas je malsamaj fazaj rapidoj en disverŝantaj mediumoj, por granda frekvenca limigo (mallarĝa koverto en spaco) la observita pulso devas ŝanĝi sian formon dum vojaĝado, farante grupan rapidon neklaran aŭ sentaŭgan kvanton.

Fizika ekzegezo

La grupa rapido estas ofte konsiderata de kiel la rapido je kiu energio aŭ informo estas alveturigata laŭ ondo. En plej parto de okazoj ĉi tio estas vera, kaj la grupa rapido povas esti konsiderata kiel la signala rapido de la ondformo. Tamen, se la ondo estas vojaĝanta tra absorba mediumo, ĉi tiu ne ĉiam veras. Ekde la 1980-aj jaroj, diversaj eksperimentoj kontrolis ke eblas por la grupa rapido de laseraj lumaj pulsoj senditaj tra speciale preparitaj materialoj grave superi la lumrapidon en vakuo. Tamen, superluma komunikado estas ne ebla en ĉi tiu okazo, pro tio ke la signala rapido restas malpli granda ol la lumrapido. Estas ankaŭ eble malpligrandigi la grupan rapidon al nulo, haltante la pulson, aŭ havi negativan grupan rapidon, farante la pulson al propagi malantaŭen. Tamen, en ĉi ĉiuj okazoj, fotonoj daŭre propagi je la atendita lumrapido en la mediumo.

Anomalia varianco okazas en areoj de rapida spektra variado kun respekto al la refrakta indico. Pro tio, negativaj valoroj de la grupa rapido okazas en ĉi tiuj areoj. Anomalia varianco ludas fundamentan rolon en atingo de dorsen propaganta kaj superluma lumo. Anomalia varianco povas ankaŭ esti uzata por produkti grupon kaj fazan rapidojn kiuj estas en malsama direktoj.

Aliaj esprimoj

Por lumo, la refrakta indico n, vakua ondolongo λ₀, kaj ondolongo en la mediumo λ estas ligitaj per

$\lambda _{0}={\frac {2\pi c}{\omega }}$

$\lambda ={\frac {2\pi }{k}}={\frac {2\pi v_{p}}{\omega }}$

$n={\frac {c}{v_{p}}}={\frac {\lambda _{0}}{\lambda }}$

La grupa rapido pro tio estas

$v_{g}={\frac {c}{n+\omega {\frac {\partial n}{\partial \omega }}}}$

$={\frac {c}{n-\lambda _{0}{\frac {\partial n}{\partial \lambda _{0}}}}}$

$=v_{p}\left(1+{\frac {\lambda }{n}}{\frac {\partial n}{\partial \lambda }}\right)$

$=v_{p}-\lambda {\frac {\partial v_{p}}{\partial \lambda }}$

$=v_{p}+k{\frac {\partial v_{p}}{\partial k}}$

Historio

La ideo de grupa rapido malsama de onda faza rapido estis unue proponita de William Rowan Hamilton en 1839, kaj la unua plena konsidero estis de John William Strutt Rayleigh en lia "Teorio de Sono" en 1877.

Grupa rapido de partikloj

Vidu ankaŭ: Hipotezo de de Broglie

Albert Einstein unua eksplikis la ondo-partikla dualeco de lumo en 1905. Louis de Broglie hipotezis ke ĉiu partiklo devus ankaŭ eksponi ĉi tian dualecon. La rapido de partiklo, li konkludis tiam (sed ĉi tio povas esti demandita hodiaŭ, vidu pli supre), devus ĉiam esti egala la grupa rapido de la respektiva ondo. De Broglie konkludis ke se la dualecaj ekvacioj jam konataj por lumo estas la samaj por ĉiu partiklo, tiam lia hipotezo devus esti vera. Ĉi tiu signifas ke

$v_{g}={\frac {\partial \omega }{\partial k}}={\frac {\partial (E/\hbar )}{\partial (p/\hbar )}}={\frac {\partial E}{\partial p}}$

kie E estas la tuteca energio de la partiklo;

p estas ĝia momanto;

$\hbar$ estas la malpligrandigita konstanto de Planck.

Por libera ne-relativisma partiklo de ĉi tio sekvas ke

${\begin{aligned}v_{g}&={\frac {\partial E}{\partial p}}={\frac {\partial }{\partial p}}\left({\frac {1}{2}}{\frac {p^{2}}{m}}\right)\\&={\frac {p}{m}}\\&=v\end{aligned}}$

kie m estas la maso de la partiklo;

v estas ĝia rapido.

Ankaŭ en speciala teorio de relativeco ni trovi (tiu, ke, kiu)

${\begin{aligned}v_{g}&={\frac {\partial E}{\partial p}}={\frac {\partial }{\partial p}}\left({\sqrt {p^{2}c^{2}+m^{2}c^{4}}}\right)\\&={\frac {pc^{2}}{\sqrt {p^{2}c^{2}+m^{2}c^{4}}}}\\&={\frac {p}{m{\sqrt {(p/(mc))^{2}+1}}}}\\&={\frac {p}{m\gamma }}\\&={\frac {mv\gamma }{m\gamma }}\\&=v\end{aligned}}$

kie m estas la kvietmaso de la partiklo;

c estas la lumrapido en vakuo;

γ estas la lorenca faktoro;

v estas la rapido de la partiklo sendistinge de onda konduto.

Grupa rapido egala al elektrona rapido devus ne esti konfuzita kun faza rapido (egala al la produto de la elektrona frekvenco kaj ĝia ondolongo).

Ambaŭ en relativisma kaj ne-relativisma kvantuma fiziko, oni povas identigi la grupan rapidon de partikla ondfunkcio kun la partikla rapido. Kvantummekaniko tre precize demonstracias ĉi tiun hipotezon, kaj la rilato estas montrita eksplicite por partikloj tiel granda kiel molekuloj.

Vidu ankaŭ

• Onda disvastigo
• Varianco (optiko)
• Faza rapido
• Antaŭa rapido
• Grupa malfruo kaj faza malfruo
• Signala rapido
• Malrapida lumo
• Onda disvastiga rapido

Referencoj

• Biot, M. A. (1957). General theorems on the equivalence of group velocity and energy transport - Ĝeneralaj teoremoj sur la ekvivalenteco de grupa rapido kaj energia transporto. Physical Review - Fizika Recenzo 105 (4) 1129–1137. COI:10.1103/PhysRev.105.1129. 1957PhRv..105.1129B].
• Whitham, G. B. (1961). Group velocity and energy propagation for three-dimensional waves - Grupa rapido kaj energia disvastigo por tri-dimensiaj ondoj. Communications on Pure and Applied Mathematics - Komunikaĵoj sur Pura kaj Aplikita Matematiko 14 (3) 675–691. COI:10.1002/cpa.3160140337.
• Lighthill, M. J. (1965). Group velocity - Grupa rapido. IMA Journal of Applied Mathematics - IMA Ĵurnalo de Aplikita Matematiko 1 (1) 1–28. COI:10.1093/imamat/1.1.1.
• Bretherton, F. P.; Garrett, C. J. R. (1968). Wavetrains in inhomogeneous moving media - Ondoserioj en nehomogenaj movantaj mediumoj, Series A, Mathematical and Physical Sciences - Serio A, Matematika kaj Fizika Sciencoj. Proceedings of the Royal Society of London - Paperoj de la Reĝa Societo de Londono 302 (1471) 529–554. COI:10.1098/rspa.1968.0034. 1968RSPSA.302..529B].
• Hayes, W. D. (1973). Group velocity and nonlinear dispersive wave propagation - Grupa rapido kaj nelineara disverŝanta onda disvastigo, Series A, Mathematical and Physical Sciences - Serio A, Matematika kaj Fizika Sciencoj. Proceedings of the Royal Society of London - Paperoj de la Reĝa Societo de Londono 332 (1589) 199–221. COI:10.1098/rspa.1973.0021. 1973RSPSA.332..199H].

Eksteraj ligiloj

• Greg Egan havas bonegan apleton en lia retpaĝaro Arkivigite je 2005-06-15 per la retarkivo Wayback Machine kiu ilustras la montreblan diferencon de grupa rapido kaj faza rapido
• Grupo kaj Faza Rapido Arkivigite je 2006-08-13 per la retarkivo Wayback Machine - apleto kun konfigureblaj grupa rapido kaj frekvenco
• Maarten Ambaum havas retpaĝon kun filmo Arkivigite je 2019-05-04 per la retarkivo Wayback Machine demonstraciantan la gravecon de grupa rapido malantaŭen laŭ la flua evoluo de veteraj sistemoj